Adat, számrendszerek, kódolás
Mi az a bináris adat? A kettes számrendszer használata az informatikában
🤔 Mi ez a kurzus? ⬇
Digitális kultúra érettségi tételek
Kidolgozott emelt szintű digitális kultúra (informatika) érettségi tételsor és Tesztkérdések!
- ⌨ Megkapod az kidolgozott érettségi tételeket
- 📑 Egy tétel 30 perc alatt tanulható, így gyorsan fel tudsz készülni az érettségire
- 👩🎓 Tudásfelmérő tesztek a fejezetek végén
- 🖥 Megkíméled magad a keresgéléstől és a tételek kidolgozása közben jelentkező bizonytalanságtól
- 👅 A kurzus teljesítése után könnyedén tudsz szóbelizni
- 🌎 Tanulj online, amikor neked kényelmes
fejezet
óra videó
db teszt
interaktív kód
tanuló
óra alatt elvégezhető
Digitális kultúra (régi nevén: informatika) érettségi előtt állsz? Keresel egy modern tételcsomagot? Akkor jó helyen jársz! Íme egy modern kidolgozású szóbeli tételcsomag.
Ábrákkal, magyarázatokkal - emelt szintű érettségire készülő diákoknak! Ha már van egy kis informatikai tudásod, és nem az alapoktól érdekelnek a fogalmak magyarázatai, akkor ez neked való!
Tartalomjegyzék
1. témakör: Tételek

1. Az internet fizikai felépítése
Megismerjük az internet kialakulásának történetét, a hálózati eszközöket, az ISDN és ADSL működését.

2. Az internet logikai működése
OSI modell, IP, MAC és csupa 2-3 betűs rövidítés magyarázata

3. Háttértárak
Lyukkártya, mágnesszalag, hajlékonylemez, CD, DVD

4. A merevlemez
Megismerjük a merevlemez működését, az adatok tárolásának, olvasásának és írásának mikéntjét.

5. Elektronikus üzenetküldés - E-mail
Az e-mail küldés működése, protokollok, DNS névfeloldás, üzenetmezők...

6. A számítógép működése
Az alaplap portjai, bővítőkártyák, CPU, utasításkészletek, buszok, memóriák...

7. Kimeneti perifériák
Megjelenítő eszközök, nyomtatók

8. Bemeneti perifériák
Megismerjük a billentyűzet, egér, érintőképernyő, képolvasók és egyéb perifériák működését

9. Internetes szolgáltatások
WWW, HTTP, HTML, DNS, protokollok, keresők és egyéb szolgáltatások.

10. Számítógépes ergonómia
Mire kell figyelni a technikai eszközök használatakor? Mi az a hardveres és szoftveres ergonómia?

11. Adat, számrendszerek, kódolás
Mi az a bináris adat? A kettes számrendszer használata az informatikában

12. Operációs rendszerek
Multitasking, az operációs rendszerek rétegei, tulajdonságai, a számítógép indulása...

13. Tömörítés
Tömörítés hatékonysága, veszteséges és veszteségmentes tömörítési algoritmusok

14. Titkosítás
Egy és kétkulcsos titkosítás, digitális aláírás magyarázata

15. Számítógépes vírusok
A vírusok típusai, védekezés a vírusok ellen, social engineering...

16. Digitalizálás
Analóg és digitális közötti különbség, a digitalizálás lépései
2. témakör: Tudástesztek

17. Az internet fizikai felépítése | Teszt
Tesztkérdések Az internet fizikai felépítése című tételhez

18. Az internet logikai működése | teszt
Tesztkérdések Az internet logikai működése című tételhez

19. Háttértárak | Tudásteszt
Tesztkérdések a Háttértárak című érettségi tételhez

20. A merevlemez | Felmérő
Tesztkérdések A merevlemez című érettségi tételhez

21. E-mail | Tesztkérdések
Tesztkérdések az Elektronikus üzenetküldés című érettségi tételhez

22. A számítógép működése | Kérdések
Tesztkérdések A számítógép működése című érettségi tételhez

23. Kimeneti perifériák | Tudásteszt
Tesztkérdések a Kimeneti perifériák című tételhez

24. Bemeneti perifériák | Tudásteszt
Tesztkérdések a Bemeneti perifériák című érettségi tételhez

25. Internetes szolgáltatások | Teszt
Tesztkérdések az Internetes szolgáltatások című érettségi tételhez

26. Számítógépes ergonómia | Teszt
A Számítógépes ergonómia című tétel tudástesztje

27. Adat, számrendszerek, kódolás | Teszt
Az Adat, számrendszerek, kódolás című érettségi tétel tudástesztje

28. Operációs rendszerek | Tudásteszt
Az Operációs rendszerek című érettségi tétel tudástesztje

29. Tömörítés | Tudásteszt
A Tömörítés című érettségi tétel tudástesztje

30. Titkosítás | Érettségi Tudásteszt
A Titkosítás című érettségi tétel tudástesztje

31. Számítógépes vírusok | Tudásteszt
A Számítógépes vírusok című érettségi tétel tudástesztje

32. Digitalizálás | Tudásteszt
A Digitalizálás című érettségi tétel tudástesztje
A kurzus anyaga folyamatosan feltöltés alatt áll - nézz vissza később még több anyagért.
Miért csatlakozz?
| Ingyenes | Regisztráció | Prémium | |
|---|---|---|---|
| 🔓 Hozzáférés a nyílt fejezetekhez | ✅ | ✅ | ✅ |
| 💻 Kódfuttatás | Demo környezet | ✅ Korlátozásokkal |
✅ |
| 🕓 Kód fordítási sebesség | 😊 6-9 sec |
😄 3-6 sec |
😜 < 3 sec |
| 🔐 Hozzáférés a zárt fejezetekhez | ❌ | ✅ | ✅ |
| 📄 Tudásfelmérő tesztek | ❌ | ✅ | ✅ |
| 📝 Hozzászólási lehetőség | ❌ | ✅ | ✅ |
| 💰 Pontgyűjtés és TOPlista | ❌ | ✅ | ✅ |
| 🎓 Hozzáférés a teljes tananyaghoz | ❌ | ❌ | ✅ |
| 🎁 Hozzáférés az összes interaktív feladathoz | ❌ | ❌ | ✅ |
| 💡 Belépés a tanulócsoportba | ❌ | ❌ | ✅ |
| 🙏 Oktatói segítség | ❌ | ❌ | ✅ |
| 💾 Letölthető összefoglaló "puska" | ❌ | ❌ | ✅ |
| 🔖 Virtuális oklevél kiállítása | ❌ | ❌ | ✅ |
Mit találsz az oldalon?
Pariatur officia labore labore magna. Irure incididunt occaecat velit incididunt ad. Dolore mollit qui adipisicing voluptate anim reprehenderit incididunt id aliquip proident. Proident dolore duis laboris ex pariatur excepteur nisi enim ut aliqua nulla magna incididunt mollit.
21. századi oktatás
Pariatur officia labore labore magna. Irure incididunt occaecat velit incididunt ad. Dolore mollit qui adipisicing voluptate anim reprehenderit incididunt id aliquip proident. Proident dolore duis laboris ex pariatur excepteur nisi enim ut aliqua nulla magna incididunt mollit.
Az online kódszerkesztőnk
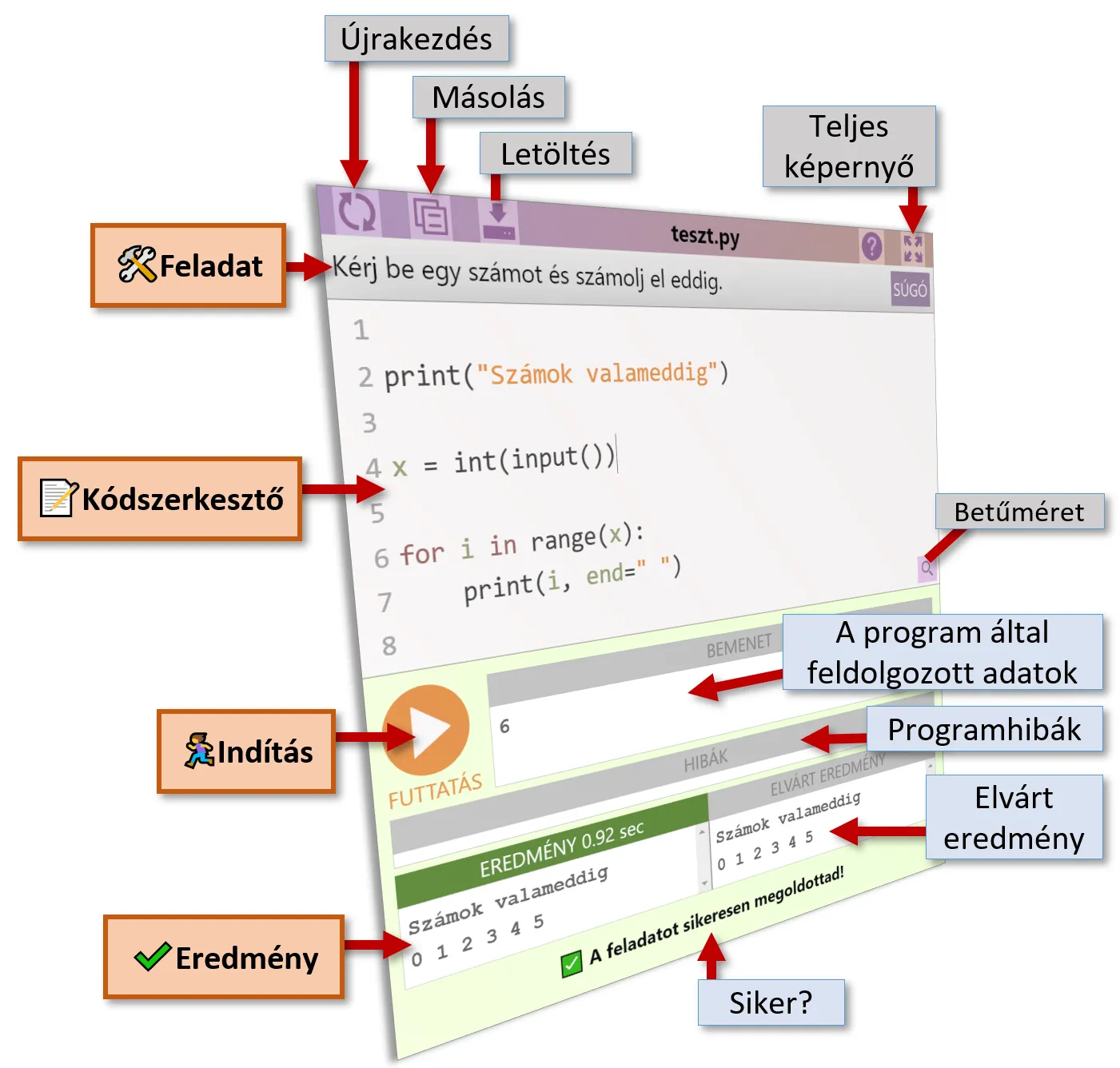
Hasonló kurzusok
Digitális kultúra érettségi tételek
Kidolgozott emelt szintű digitális kultúra (informatika) érettségi tételsor és Tesztkérdések!
C programozás kezdőknek
Tanulj teljesen interaktív környezetben C programozást. A kurzusban elsajátíthatod az alapokat, ami szükséges az induláshoz.
Digitális képszerkesztés GIMP-pel
Tanuld meg a digitális képszerkesztést a legnépszerűbb Photoshop-szerű programban!
3D modellezés és animáció Blender-ben
Tanuld meg a 3D modellezés alapjait és alkoss lenyűgöző virtuális világokat!