🤔 Mi ez a kurzus? ⬇
C programozás kezdőknek
Tanulj teljesen interaktív környezetben C programozást. A kurzusban elsajátíthatod az alapokat, ami szükséges az induláshoz.
- ⌨ Interaktív kódszerkesztő, önmagát kijavító feladatok
- 👩🎓 Tudásfelmérő tesztek a fejezetek végén
- 🖥 Visszanézhető oktatóvideók
- 📑 Szuper izgalmas jegyzetek
- 👅 Magyar nyelvű
- 🌎 Tanulj online, amikor neked kényelmes
// Át is tudod írni a kódot!
#include<stdio.h>
int main(){
printf("Hello vilag!\n");
for(int i=0; i<6; i++)
printf("%d ",i);
return 0;
}c
42
Hello vilag! 0 1 2 3 4 5 Hello vilag! 0 1 2 3 4 5 teszt.c Ez itt egy interaktív kódszerkesztő. Kattints a futtatás gombra! Online tudsz progamozni. Írd át kódot.
fejezet
óra videó
db teszt
interaktív kód
tanuló
óra alatt elvégezhető
A legtöbb programozási nyelv ősanyja a C nyelv. Így ennek megtanulása alapvető fontosságú az informatikai előmenetel szempontjából.
A Windows operációs rendszer is C-ben illetve C++-ban íródott. Ebben a kurzusban megismerheted a programozás alapjait a C nyelven keresztül. Nem szükséges informatikai előképzettség, az alapoktól kezdve ismered meg a kódolás mikéntjét.
Tartalomjegyzék
1. témakör: Alapok

1. A programozás rejtelmes világa
Megtudjuk mi az a gépi kód, az assembly és hogy milyen részei vannak a fejlesztőkörnyezetnek.

2. A fejlesztőkörnyezet
Letöltjük és beállítjuk a Code::Blocks fejlesztőkörnyezetet.

3. Mi a tök az a C nyelv?
Megtudjuk hol helyezkedik el a C nyelv a programnyelvek világában.
2. témakör: Ideje kódolni!

4. Hello világ!
Megírjuk az első programunkat.

5. A programkód részei
Elemezzük a program részeit.

6. Pompás feladatok
Megismerjük a vezérlőkaraktereket és a kommenteket.
3. témakör: Adattárolás a memóriában

7. A változó
Kiírási tudományunkat továb fejlesztjük, és megtudjuk mi az a hely-jelölő.

8. Valós változók
A valós számok eltárolása

9. Játék a határokkal
A változók típusmódosítói

10. Karakterek
Megismerjük a karakter változót
4. témakör: Beszélgessünk a felhasználóval

11. Beolvasás
Adatokat kérünk a felhasználótól

12. Hasznos feladatok
Érdekes és hasznos szoftvereket írunk: fizikai számításokat végzünk (út-idő-sebesség, fahrenheit-celsius konvertálás).

13. Feladat: Cipőméret
5. témakör: Döntsön a program

14. Az IF feltétel
Írunk egy gondolkozó programot. Kész a jövő Terminátora.

15. A gondolkodó program
Gyakorló feladatok az IF programszerkezettel kapcsolatban.

16. Az algoritmus
Megtudjuk mi az az algoritmus és hogyan lehet leírni.

17. Feladat: Skandalum vagy Imbecil?
Az eddigi tananyagra alapozó önálló feladat
6. témakör: Ismétlés a kód anyja

18. FOR ciklus
Megtudjuk hogyan lehet dolgokat ismételni a programkódban

19. A ciklusos dolgok bedurvulnak
A végtelen ciklus és az egymásba ágyazás

20. Ciklusos feladatok
Érdekes feladatok a FOR ciklus felhasználásával

21. Feladat: Hurránaptár!
Kihívás: Készíts naptárgeneráló programot!
7. témakör: Prímszámkereső

22. Prímszámkereső rávezetés
Megoldunk 3 feladatot, ami a prímszámkereső megértéséhez segít minket

23. Prímszámkereső írás
Megírjuk a prímszámkeresőt

24. Prímszámkereső tuning
Kétszeresére gyorsítjuk a prímszámkeresőt
8. témakör: Szövegkezelés

25. Tömbök
Karakterekből karakterláncokat építünk.

26. Whitespace és képernyőtörlés
Megismerjük a printf alternatíváját és hogy hogyan kell képernyőt törölni

27. Szöveg hossza és fényújság
Megismerünk egy hasznos könyvtári függvényt és megcsinálunk egy izgalmas feladatot
9. témakör: Fájlkezelés
A kurzus anyaga folyamatosan feltöltés alatt áll - nézz vissza később még több anyagért.
Miért csatlakozz?
| Ingyenes | Regisztráció | Prémium | |
|---|---|---|---|
| 🔓 Hozzáférés a nyílt fejezetekhez | ✅ | ✅ | ✅ |
| 💻 Kódfuttatás | Demo környezet | ✅ Korlátozásokkal |
✅ |
| 🕓 Kód fordítási sebesség | 😊 6-9 sec |
😄 3-6 sec |
😜 < 3 sec |
| 🔐 Hozzáférés a zárt fejezetekhez | ❌ | ✅ | ✅ |
| 📄 Tudásfelmérő tesztek | ❌ | ✅ | ✅ |
| 📝 Hozzászólási lehetőség | ❌ | ✅ | ✅ |
| 💰 Pontgyűjtés és TOPlista | ❌ | ✅ | ✅ |
| 🎓 Hozzáférés a teljes tananyaghoz | ❌ | ❌ | ✅ |
| 🎁 Hozzáférés az összes interaktív feladathoz | ❌ | ❌ | ✅ |
| 💡 Belépés a tanulócsoportba | ❌ | ❌ | ✅ |
| 🙏 Oktatói segítség | ❌ | ❌ | ✅ |
| 💾 Letölthető összefoglaló "puska" | ❌ | ❌ | ✅ |
| 🔖 Virtuális oklevél kiállítása | ❌ | ❌ | ✅ |
Mit találsz az oldalon?
Pariatur officia labore labore magna. Irure incididunt occaecat velit incididunt ad. Dolore mollit qui adipisicing voluptate anim reprehenderit incididunt id aliquip proident. Proident dolore duis laboris ex pariatur excepteur nisi enim ut aliqua nulla magna incididunt mollit.
21. századi oktatás
Pariatur officia labore labore magna. Irure incididunt occaecat velit incididunt ad. Dolore mollit qui adipisicing voluptate anim reprehenderit incididunt id aliquip proident. Proident dolore duis laboris ex pariatur excepteur nisi enim ut aliqua nulla magna incididunt mollit.
Az online kódszerkesztőnk
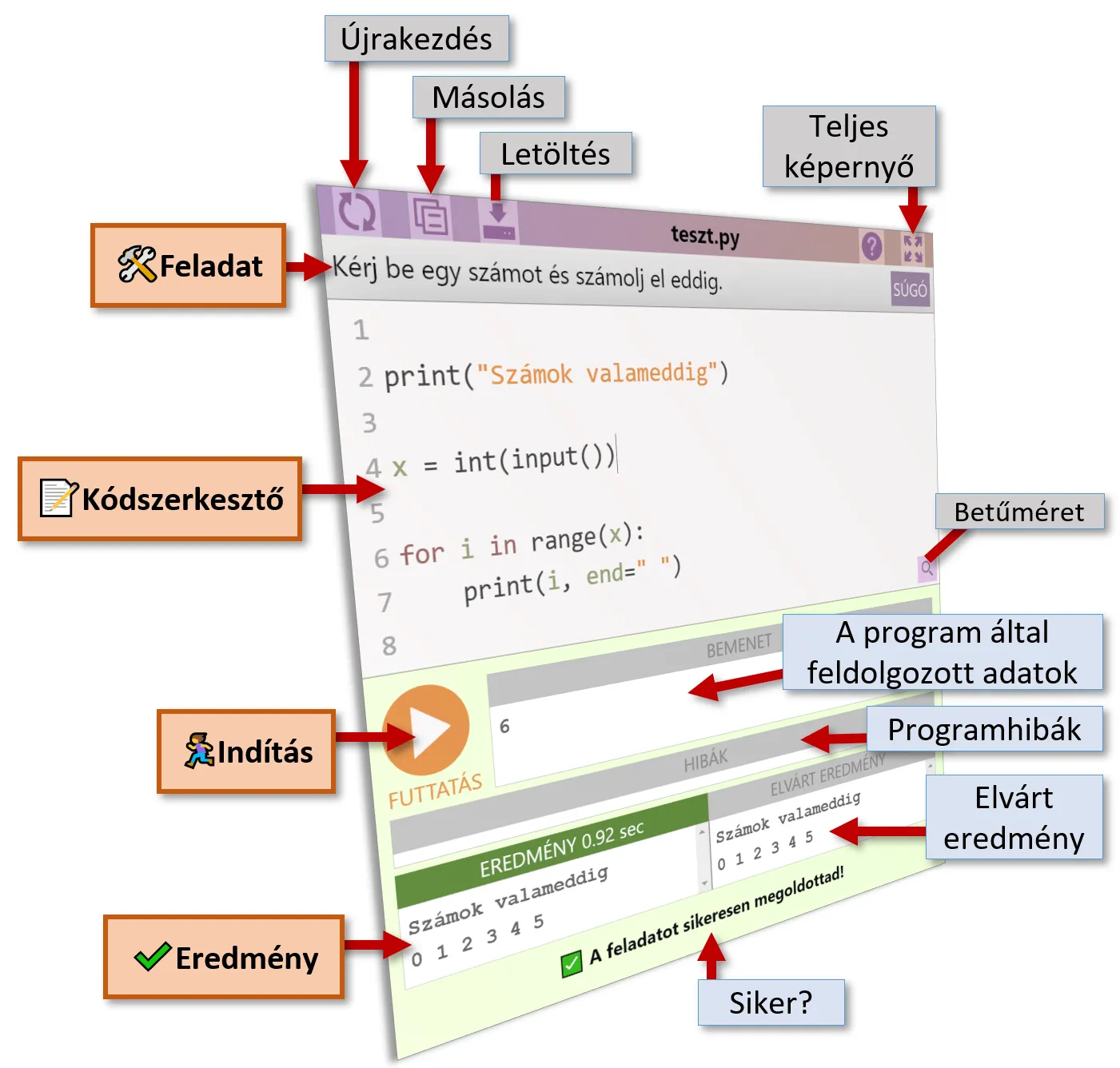
Hasonló kurzusok
Digitális kultúra érettségi tételek
Kidolgozott emelt szintű digitális kultúra (informatika) érettségi tételsor és Tesztkérdések!
C programozás kezdőknek
Tanulj teljesen interaktív környezetben C programozást. A kurzusban elsajátíthatod az alapokat, ami szükséges az induláshoz.
Digitális képszerkesztés GIMP-pel
Tanuld meg a digitális képszerkesztést a legnépszerűbb Photoshop-szerű programban!
3D modellezés és animáció Blender-ben
Tanuld meg a 3D modellezés alapjait és alkoss lenyűgöző virtuális világokat!